논문 제목 : Decoupled Knowledge Distillation
Contribution
- 기존 KD를 TCKD(Target Class Knowledge Distillation), NCKD(Non-Target Class Knowledge Distllation) 로 나누어 logit distllation의 insight 제공
- 한쌍의 공식으로 되어있는 기존 KD Loss의 한계점을 드러냄.
- Teacher의 Confidence Score와의 Coupling NCKD로 지식 전이의 효과가 억압됨. 그리고 TCKD와 NCKD의 결합은 두 부분의 균형 유연성을 제한시킴
- 효과적인 logit Distillation DKD를 제안
- Feature-based Distillation 방법과 비교해서 DKD의 feature 전이성의 효율성을 검증
Related Works
- 기존 연구는 2가지 타입으로 분류됨
- Dislltation from logits
- 새로운 방법론을 내세우기 보다는 효과적인 규제 방법, 최적화 방법에 초점이 맞춰짐
- DML은 상호적인 학습으로 student와 teacher를 동시에 학습하였음
- TAKD는 중간 크기의 신경망을 제안하여 Teacher의 조수 역할을 하여 Teacher와 Student 간의 Gap을 좁혀주는 역할을 하였음
- 반면에 몇몇 연구들은 기존 KD 방법의 해석에 초점을 맞춤
- Intermediate feature
- SOTA 연구들은 중간 feature 기반으로 연구가 이루어짐. 이는 Teacher로부터 Student가 표현력을 직접적으로 전이하기 위해서임
- 혹은, Teacher 안의 샘플 사이의 상관관계를 Student에 전이하는 방식임
- 대부분의 Feature 기반 방법들은 Logit-based Method에 비해 높은 성능을 보임
- 다만, 상당한 연산량과 저장소 비용이 요구됨
- Dislltation from logits
- 본 논문은 어떤 것이 잠재적인 logit 기반 방법을 제한하는지 분석하고 logit 방법을 재활성화
Rethinking KD
- KD Loss를 재공식화
- Target Class 따로, Non-Target Class 따로
- KD 프레임워크에서 각 파트의 효과를 조사하고 기존 KD의 한계점 조사.
- 이런 조사를 영감받아 새로운 logit distllation 방법을 제안
- Target과 Non-Target을 분리하기 위해 아래와 같은 notation을 정의
$$ \mathbf{b} = [p_t,p_{\backslash t}] \in \mathbb{R}^{1\times2} $$
- 위는 binary probabilites로 Target Class p_t와 Non Target Class p_\t를 나타냄
$$ p_t = \frac{\mathsf{exp}(z_t)}{\sum^{C}{j=1}\mathsf{exp}(z_j)} , p{\backslash t} = \frac{\sum^{C}{k=1, k\neq t}\mathsf{exp}(z_j)}{\sum^{C}{j=1}\mathsf{exp}(z_j)} $$
- 즉 p_t는 target에 대한 확률 분포를 나타내며
- p_\t는 target을 제외한 나머지 non-target에 대한 확률 분포를 표현한 것임
- 이를 토대로 non-targe t class의 모델 확률 분포를 표현하면 아래와 같이 표현됨
$$ \hat{p_i} = \frac{\mathsf{exp}(z_i)}{\sum^{C}_{j=1, j\neq t}\mathsf{exp}(z_j)} $$
- p_hat_i는 non-target probabilities를 나타내며, p_hat_i는 p_t / p_\t 와 같은 꼴이 됨.
Reformulation
- 앞서 언급한 binary probabilities b와 non-target classes p_hat로 KD를 재공식화.
- 먼저, 기존 방식의 KL Divergence는 아래와 같은 수식으로 나타내짐
$$ \mathbf{KD} = \mathbf{KL}(\mathbf{p^\mathcal{T}||p^\mathcal{S})} = p_t^\mathcal{T} \mathsf{log}(\frac{p_t^\mathcal{T}}{p_t^\mathcal{S}}) + \sum^C_{i=1, i\neq t} p_i^\mathcal{T} \mathsf{log} (\frac{p_i^\mathcal{T}}{p_i^\mathcal{S}}) $$
- 결국 Teacher와 Student의 KL loss는 Target에 대한 KL Loss 와 Non-Target에 대한 KL Loss를 더한 과정임.
- 재구성해서 나온 최종적인 KD는 다음과 같다
$$ \mathbf{KD} = \mathbf{KL}(\mathbf{b^\mathcal{T}} || \mathbf{b^\mathcal{S}}) + (1-p_t^\mathcal{T})\mathbf{KL}(\hat{\mathbf{p}}^\mathcal{T} || \hat{\mathbf{p}}^\mathcal{S}) $$
- KD Loss는 위와 같이 두 가지의 weighted sum 형태로 재공식화된다.
- 전자의 수식은 Teacher와 Student의 Target Class의 binary probabilities 유사성임
- 후자의 수식은 Teacher와 Student의 Non-Target Class의 확률 분포 유사성임
- 논문은 이러한 2가지 유사성에 대해 아래와 같이 재표현함
- NCKD는 p_t^T의 가중치 역할로 묶여있음.
Effects of TCKD and NCKD
- ResNet, WideResNet(WRN), ShuffleNet을 traning 모델로 삼음.
- Result (1) : Student baseline
- Result (2) : 기존 Kd(TCKD와 NCKD 융합)
- TCKD보다는 좋을때도 있고 나쁠때도 있음
- Result (3) : singly TCKD
- 성능 결과가 그렇게 좋진 않음. 오히려 떨어지는 경우도 있음
- p_t^T(Teacher Confidence Score)가 0.99일때는 데이터가 쉽다는 것이며, 0.75는 상대적으로 어려운 상황을 이야기함
- difficulty 라는 지식을 제공하는 것이 TCKD의 메인 목적
- 더 어려운 traning data가 주어질때 TCKD는 이득을 더 줄 수 있을 것임
- 결국, Strong Augumentation(기존 rotate와 같은 augumentation은 weak Augumentation)의 원본 이미지 훼손 정도가 심해지면, 더 좋은 성능을 보임
- 논문은 AutoAugment으로 훼손정도를 크게하여 TCKD의 성능을 묘사함
- AutoAugment는 AutoML처럼 RNN Controller로 데이터 증식 방안을 스스로 도출하여 데이터 증식 시키는 방법론임
- ImageNet으로 수행한 실험에서도 더 개선된 효과를 보임
- (여기서 해볼 수 있는 실험. 엄청 쉬운 MNIST에 대해서는 얼마나 성능이 떨어질 수 있을지?)
- Result (4) : singly NCKD
- 기존 KD 보다 좋은 성능을 보임
- 실험을 통해, Non-taret Classes에 대한 지식 증류는 logit distillation에서 중요한 요소로 입증함.
- p_t^T가 Teacher의 Target Class에 대한 Confidence score인데, 이는 NCKD와 묶여 가중치 역할을 수행함을 주목해보았을때,
- NCKD의 가중치가 더 작을 때 더 좋은 예측을 봄.
- (Confidence Score가 높으면 Softmax로 나오는 정답의 확률값이 높다는 의미)
- 실험을 기반으로 한 가정은 Teacher가 training Sample에 대해 더 Confident하다면, 더 신뢰할만하며 귀중한 지식을 제공할 수 있을 것임. 하지만, loss weight는 confident 에 의해 억압됨
- 이에 대한 검증 실험으로, p_t^T로부터의 training sample 랭킹을 매겨볼 것임
- one sub-set은 top-50% sample이 포함되며, 나머지 샘플은 다른 sub-set에 포함될 것임.
- 결국, Teacher가 잘 예측한 top-50% 샘플 및 그외 샘플 가지고 실험을 진행한다는 것임
- Teacher가 잘 예측한 샘플들은 다른것들에 비해 지식이 풍부할 것이지만, 실험결과 오히려 Teacher의 높은 confidence에 의해 top-50% 데이터의 loss weight은 억압되면서 성능이 저하됨
- 당연하다고 느껴지는게, 높은 Confidence Score를 가진 Sample이라면 나머지 Non-Target에 대한 확률 분포는 상대적으로 더 작은 값을 가지게 될것임
- 좋은 정보를 가진 Sample이여도 NCKD 관점에서는 Non-target에 대해서 더 초점이 맞춰져있기 때문에 더 적은 Confidence Score도 포함된 데이터로 학습해야 좋은 성능이 나타날 것같음
Decoupled Knowledge Distillation(DKD)
- KD loss를 TCKD 와 NCKD로 나눴었음
- TCKD는 traning Sample의 Difficulty 지식을 전달해서 어려운 task를 더 잘 해냄
- NCKD는 (1-p_t^T) 가 낮은 조건일때 non-target class의 지식 전이가 더 억제되는것을 알 수 있었음
- 1-p가 낮다는 것은 confidence score가 높을 때를 의미
- NCKD는 1-p 와 묶여 있어서 Confidence Score가 높은 샘플이 더 좋은 정보를 가져오지만, 묶여 있어서 효과에 제한걸림
- NCKD와 TCKD가 기존 KD 프레임워크 내에서 묶여있기 때문에 나눠서 중요성 균형을 위해 가중치를 바꾸는게 허용이 안됨
- 논문은 TCKD와 NCKD가 분리되어야한다고 함
- 따라서, 분리된 KD, Decoupled KD를 제안하며 이에 대한 loss function은 다음과 같음
$$ \mathbf{DKD} = \alpha\mathbf{TCKD} + \beta\mathbf{NCKD} $$
- 기존 1-p를 beta로 교체하고 TCKD 와 NCKD의 중요성을 alpha와 beta로 조정가능하도록 하였음
Main Results
- Result (1) : NCKD와 1-p의 분리 성능 결과
- Ablation Study - 1-p 제거했을때와 beta 혹은 alpha를 붙였을때의 성능 차이
- Result (2) : NCKD와 TCKD 의 분리 성능 결과
- Training Efficiency를 보면 다음 그림과 같다.
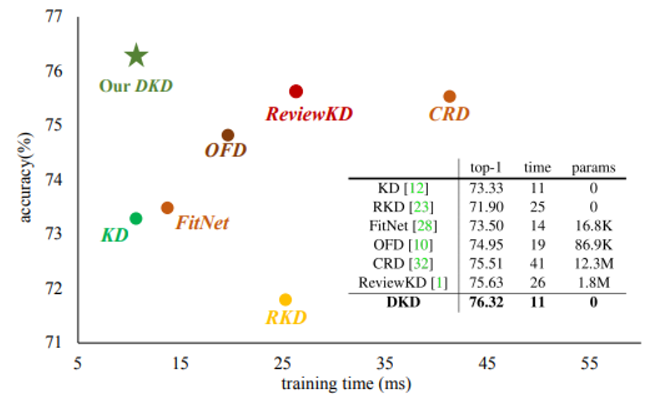
- 기존 KD의 재공식화했기 때문에 같은 연산 복잡성을 가지며, 추가 파라미터가 필요하지않다. Feature based와 비교가 됨
'논문 리뷰' 카테고리의 다른 글
| Class-aware Information for Logit-based Knowledge Distillation 논문 리뷰 (5) | 2024.03.08 |
|---|---|
| Distilling Knowledge via Knowledge Review 논문 리뷰 (2) | 2024.02.29 |
| GCN paper review (0) | 2023.06.02 |
| GCN paper review 전 공부 - semi-supervised learning (0) | 2023.05.30 |
| MobileNet paper review (0) | 2023.02.08 |